• V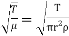ELOCITY OF SOUND WAVE IN STRINGS: The velocity, V of a sound wave in strings is given by the expression.

V= , = mass per unit length or linear density =

Where r =radius of the wire, = density of material of the string or wire and T = tension

• VELOCITY OF SOUND WAVE IN SOLIDS

The velocity, V of a sound wave in a solid is given by the expression:

Where E = Young’s modulus of the material, = density of the solid or material.

• VELOCITY OF SOUND WAVE IN LIQUID

The velocity, V of a sound wave in a liquid is given by the expression:

Where B = Bulk Modulus of the liquid, = density of the liquid.

• VELOCITY OF SOUND WAVE IN A GAS

The velocity, V of a sound wave in a gas is given by the expression

Where M = molecular mass, R = molar gas constant, = ratio of the two specific heat capacities of a gas, P = pressure and = density

• VELOCITY OF WATER WAVE

For deep water waves, V =

For shallow water waves, V=

For surface ripples, V =

Where = wavelength, d = depth of water, = surface tension, =density of water, g = acceleration due to gravity.

The Harmonic Oscillator

Consider a simple pendulum consisting of a mass-less string of length ‘l’ and a point like object of mass ‘m’ attached to one end called the bob. Suppose the string is fixed at the other end and is initially pulled out at an angle from the vertical and released from rest from the figure below. Neglect any dissipation due to air resistance or frictional forces acting at the pivot.

Diagram

Note

• Is defined with respect to the equilibrium position.
• When, the bob has moved to the right.
• When, the bob has moved to the left.

Coordinate system free-body force diagram

Tangential component of the gravitational force is

(1)

Note

• The tangential force tends to restore the pendulum to the equilibrium value. If and if .
• The angle is restricted to the range .
• the string would go slack.

The tangential component of acceleration is

(2)

Newton’s second law, , yields

(3)

T= (4)

Simple Harmonic Motion

Diagram

The object is attached to one end of a spring. The other end of the spring is attached to a wall at the left in the figure above. Assume that the object undergoes one-dimensional motion.

The spring has a spring constant k and equilibrium length (l).

Note

• x>0 corresponds to an extended spring.
• x<0 corresponds to a compressed spring.

Therefore

(5)

Newton’s second law in the x-direction becomes

(6)

Equation 6 is called the simple harmonic oscillator equation. Because the spring force depends on the distance x, the acceleration is not constant.

• is constant of proportionality

Energy in Simple Harmonic Motion

Diagram

(7)

(8)

It is easy to calculate the velocity for a given t value

(9)

And the energy associated with

(10)

A stretched or compressed spring has certain potential energy.

Diagrams

( Hooke’s law) in order to stretch the spring from O to X one need to do work; the force changes, so we have to integrate:

W= (11)

Note

This work is stored in the spring as its potential energy U.

So, for the oscillator considered, the energy U is:

U=

(12)

Therefore, the total energy is:

(13)

(14)

(15)

(16)

Equation (16) is a famous expression for the energy of a harmonic oscillator.

Note

• Where A is the maximum displacement. The total energy is constant in time(t), but there is continuous process of converting to kinetic energy to potential energy, and then K back to U. K reaches maximum twice every cycle (when passing through x=0)’ and U reaches maximum twice, at the turning point.

Diagram0

In this graph time(t) was set to zero when the mass passed the x=0 point.

Finally, we can use the principle of conservation of energy to obtain velocity for an arbitrary position by expressing the total energy position as

(17)

(18)

(19)

Example 1

A 200g block connected to a light spring for which the force constant is 5.00N/m is free to oscillate on a horizontal, frictionless surface. The block is displaced 5.00cm from equilibrium and released from rest.

• Find the period of its motion
• Determine the maximum speed of the block
• What is the maximum acceleration of the block?
• Express the position, speed and acceleration as function of time.

Example 2

A 0.500Kg cart connected to a light spring for which the force constant is 20.0N oscillates on a horizontal, frictionless air track.

• Calculate the total energy of the system and the maximum speed of the cart if the amplitude of the motion is 3.0cm
• What is the velocity of the cart when the position is 2.00cm?
• Compute the kinetic energy and the potential energy of the system when the position is 2.00cm.

Energy in waves

Note

Waves transport energy when they propagate through a medium. Consider a sinusoidal wave travelling on a string. The source of the energy is some external agent at the left end of the string, which does work in producing the oscillations. We can consider the string to be a non-isolated system. As the external agent performs work on the end of the string, moving it up and down, energy enters the system of the string and propagates along its length.

Let us focus our attention on an element of the string of length and mass . Each element moves vertically with SHM. Thus, we can model each element of the string as simple harmonic oscillator (SHO), with the oscillation in the y direction. All elements have the same angular frequency and the same amplitude A. The kinetic energy K associated with a moving particle is:

K= (20)

If we apply this equation to an element of length and mass, we shall see that the kinetic energy of this element is

(21)

is the transverse speed of the element.

If is the mass per unit length of the string, then the mass of the element of length is equal to. Hence, we can express the kinetic energy of an element of the string as

(22)

As the length of the element of the string shrinks to zero, this becomes a differential relationship:

(23)

Using the general transverse speed of a simple harmonic oscillator

(24)

(25)

(26)

If we take a snapshot of the wave at time t=0, then the kinetic energy of a given element is:

(27)

Let us integrate this expression over all the string elements in a wavelength of the wave, which will give us the total kinetic energy in one wavelength:

(28)

(29)

(30)

(31)

(32)

Note

In addition to kinetic energy, each element of the string has potential energy associated with it due to its displacement from the equilibrium position and the restoring forces from neighbouring elements. A similar analysis to that above for the total potential energy in one wavelength will give exactly the same result:

(33)

The total energy in one wavelength of the wave is the sum of the potential energy and kinetic energy

(34)

(35)

As the wave moves along the string, this amount the energy passes by a given point on the string during a time interval of one period of the oscillation. Thus, the power, or rate of energy transfer, associated with the wave is:

(36)

(37)

(38)

(39)

Note

This expression shows that the rate of energy transfer by a sinusoidal wave on a string is proportional to

• The square of the frequency
• The square of the amplitude
• And the wave speed.

Put differently, Is the rate of energy transfer in any sinusoidal wave that is proportional to the square of its amplitude.

Example

A taut string for which is under a tension of 8.00N.How much power must be supplied to the string to generate sinusoidal waves at a frequency of 60.0Hz and an amplitude of 6.00cm?

STANDING WAVES

Stationary Waves

Stationary wave is produced if the waveform does not move in the direction of either incident or the reflected wave. Alternatively, it is a wave formed due to the superposition of two waves of equal frequency and amplitude that are travelling in the opposite directions along the string.

Note

• You can produce stationary wave on a rope if you tie one end of it to a wall and move the free end up and down continuously. Amazingly the superposition of the incident wave and the reflected wave produces the stationary wave in the rope.
• A standing wave is produced when a wave that is travelling is reflected back upon itself.
• Antinode is an area of maximum amplitude

• Node is an area of zero amplitude.

COMPARISON BETWEEN PROGRESSIVE (TRAVELLING) WAVE AND STATIONARY (STANDING) WAVE.

PROGRESSIVE WAVE	STATIONARY WAVE
It is an advancing wave that moves in the medium continuously with a finite velocity	There is no advancement of the in any direction.
Energy flows across every plane in the direction of propagation of the wave.	There is no flow of energy across any plane.
No particle of the wave is permanently at rest.	Nodes are permanently at rest.

Example3

A wave is given by the equation y= 10sin2. Find the loop length frequency, velocity and maximum amplitude of the stationary wave produced.

solution