Centre of Mass Impact on Roll of Dice
Harrison Back

In physics, the centre of mass is defined as “The unique part in an object or system which can be used to describe the system’s response to external forces and torques” (Center of Mass, Hyperphysics.com). It references the overall average mass of an object and assigns that average to a point on or within the object, usually near the centre. This can be seen in Figure 1. Changing the location of the centre of mass affects how the object reacts to external forces. This can be seen though the object’s rotational axis.
An object’s rotational axis is the theoretical line drawn through an object to show how it will rotate. Unless an axle is deliberately created, an object will attempt to rotate around its centre of mass. This can be shown in Figure 2. As pictured, the bat’s centre of mass is closer to the end than it is the handle. As the path it draws as it circles through the air traces the travel of the centre of mass, the bat appears to spin around in an erratic manner. The path drawn shows the bat circling its rotational axis, which is in the same position as its centre of mass. 


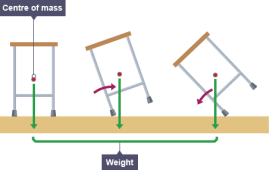
Another result of the location of the centre of mass of an object is its stability. The closer to the ground an object’s centre of mass is, the susceptible to being tipped over it is. This is why professional fighters always recommend you get down low to the ground. In order for an object to successfully be tipped over, its centre of must be moved to a position in front of the base of an object. This can be seen in Figure 3. 
When it comes to (fair) dice, the centre of mass is in the exact centre of the object. This means all the faces are equidistant from it. The result of this is, after a roll, every face has equal opportunity to come up. However, if the centre of mass is moved from the geographical centre of the dice, then the axis of rotation is changed, and the dice is no longer fair. This is known as ‘weighting’ the dice, as it is done by making one face effectively heavier than another, causing the opposite face to roll more frequently. In the following experiment, the degree to which weighting two dice affects their average roll.
The centre of mass of a cube with uniform density is at the geographical centre of the cube. Because of this, only relatively simple math is necessary to locate it. If the dice edge length is equal to 10 centimetres, then the following reasoning would indicate the geographical centre:
a2 + b2 = c2
52 + 52 = 7.0712
52 + 7.0712 = 8.6602
This means that the diagonal length between two opposite corners is equal to 8.66 centimetres, and as the geographical centre falls at the midway point on that line, the centre of mass for that object would be exactly 4.33 centimetres along the longest diagonal line.
As the dice being discussed in this experiment are 1cm3, the above calculations can be scaled back by one decimal place to give an end result of 0.433cm along the diagonal line.
Unfortunately, these calculations only hold true in the situation where the object has uniform density. As melting the dice will change the density throughout the dice, it is nearly impossible to find the exact centre of mass of the adjusted dice, as one would need to know exactly how dense any portion of the dice is.
As the centre of mass is moved further from the middle of the dice, the effectively lighter face will roll upwards more often than not.
Firstly, two six-sided dice were rolled 100 times by the same person to record a baseline to compare against. The same dice were used throughout the experiment for consistency’s sake, and the same person rolled the dice every time so as to keep a relatively continuous roll style. After this control was set, the dice were placed ‘one’ side-down on an oven tray, so as to make that side heavier and thus theoretically cause a ‘six’ to be rolled more frequently. They were then moved into an oven which had been preheating at 180° Celsius for five minutes and left to bake for an additional five minutes. These times were chosen because, in the case of the former, five minutes provided adequate time for the oven to get to temperature, while also not expending unnecessary time, and in the case of the latter, 5 minutes supplied ample time for the dice to become viscous enough to change their centre of mass, while still maintaining a somewhat cubic shape. Of course, they couldn’t be expected to remain perfectly cubic, however, they were to remain cubic enough that they could be easily mistaken as such by a casual onlooker. After the heat treatment, the same dice were rolled by the same person 100 times and the average roll was determined. This was then compared against the initial control group and a conclusion was drawn thusly.
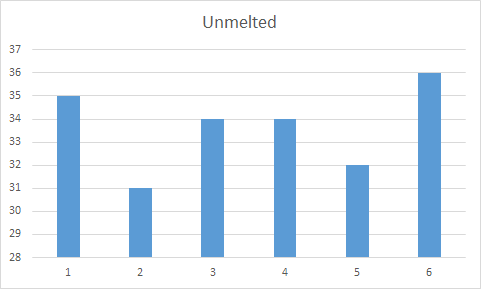
.Average: 3.46
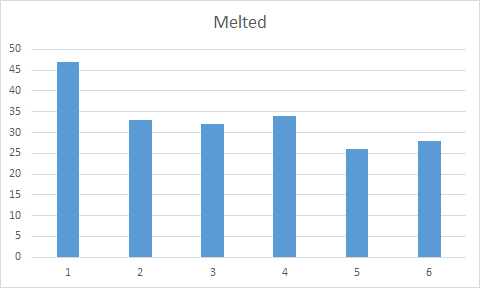
Average: 3.22
Unexpectedly, melting the dice so as to lower their centre of mass did not yield the expected result. In fact, even though it was expected that the melted dice would roll a six more frequently, the opposite occurred instead; ones were rolled more frequently than before the melting. This can be seen through the lowered average after the melting, from 3.46 to 3.22. Every piece of background research would suggest that lowering the centre of mass would cause that side to roll downwards more frequently. This means that it was most likely not a flaw in the hypothetical realm, rather one in the practical. The various uncontrollable variables, as well as recommendations should this experiment be repeated, will be discussed further below, in the Evaluation portion of this report.
There were many instances in this experiment which could have corrupted the results and caused the hypothesis to not be supported. These include, but are not limited to, the fact the dice were melted by a relatively uncontrollable heat source, the method by which they were rolled, the surface on which they were rolled, and the fact that the dice were not preserved perfectly as they were during the time between the initial, pre oven rolls, and the final, post oven rolls.
As the only apparatus available for use with melting dice that was available was a standard kitchen oven, it’s use could have caused unexpected results. The temperature was not perfectly monitored; rather it was presumed to be approximately 180° Celcius.
The surfaces the dice were rolled on varied between their pre-oven and post-oven states. Before they were melted, the dice were rolled on a hard, synthetic laminate, while, afterward, they were rolled onto a softer, malleable desk mat made from fabric and a plastic polymer. This could have resulted in differing roll averages, as the softer surface absorbed more kinetic energy from the falling dice, thus reducing the duration of their roll.
During the time between where the dice were unchanged and where they were, they were kept in one of three places. These included a compartment in a school bag, the pocket of a pair of formal pants, and open on a glass desk. This resulted in the dice being moved frequently, interacting and possibly reacting with surrounding elements, as well as each other. The throes of everyday wear could very well have caused minute damages and changes in the dice which could have lead to inaccurate results from them.
In summary, if this experiment were to be replicated, several changes would have to be made to the methodology. Firstly, a finely controlled and monitored oven would have to be used. This would result in a more deliberately variable melt; one could precisely decide how much the dice should be exposed to the heat. Also, a robotic arm should be used in place of a human one. The dice should have specific receptacles by which their roll begins the exact same way every time, and the arm (while still having some degree of variability) would be far more specific with its rolling method. The dice should remain in an airtight, pressurised container. This would function to keep the dice in as pristine condition as possible, and reduce interaction with eroding compounds to a minimum. The dice should be rolled onto a specific surface, and its properties should be closely documented and monitored. Lastly, the experiment should be done in one sitting, as prolonging it increases the risk of a change occurring in any of the many points of failure throughout the procedure.
As a result of the experiment being performed in such imprecise ways, the results were different to what was expected. However, as is the case with many high school science experiments, the necessary precision required for this kind of procedure caused inaccuracies in the experimental process and resulted in an unsupported hypothesis. As the background research supported the aforementioned hypothesis, the only plausible fault is as a result of the imperfect nature of the experiment.
Work Cited
- (‘Center of Mass’)
“Center of mass”. Hyperphysics.phy-astr.gsu.edu. N.p., 2017. Web 8 Feb. 2017 - (‘Center Of Mass’)
“Center Of Mass”. En.wikipedia.org. N.p., 2017. Web 1 Mar. 2017 - (“Torque And Angular Momentum | Physics | Science |Khan Academy”)
“Torque And Angular Momentum | Physics | Science |Khan Academy”. Khan academy. N.P., 2017. Web. 1 Mar. 2017 - (Socratic.org, 2017)
Socratic.org, (2017). Why is the center of mass important in physics> | Socratic. [online] Available at: https://socratic.org/questions/why-is-the-centre-of-mass-important-in-physics [Accessed 1 Mar. 2017]. - (Bbc.co.uk, 2017)
Bbc.co.uk. (2017). BBC – GCSE Bitesize Science – Moments : Revision, Page 4. [online] Available at: http://www.bbc.co.uk/schools/gcsebitesize/science/triple_aqa/using_physics_make_things_work/moments/revision/4/ [Accessed 1 Mar. 2017]. - Farside.ph.utexas.edu. (2017). Centre of mass. [online] Available at: http://farside.ph.utexas.edu/teaching/node102.html [Accessed 18 Mar. 2017]















